Constraints of Spacetime
If you visualize the ‘world’ from the perspective of an operand flowing through a machine, you realize that a physical machine creates a specific spatial constraint for the movement of data. Processing nodes are fixed in space, and information is exchanged between nodes to accomplish some transformation. Nodes consume and generate information, and communication links move information (program and data) between nodes. This leads to a simple abstraction of a physical parallel machine consisting of a fixed graph in space that constraints computation and communication events generated by the parallel algorithm.
Just like it takes time to compute, it takes time to communicate. In an expression, $c = a + b$, we implicitly know that the add operation takes some time to complete. However, the assignment operation, which represents the exchange of information and is equivalent to the communication phase, takes time just the same. The time relationship between computation and communication delay impacts the structure of an optimal parallel algorithm.
Technology impacts the performance of both computation and communication, but in very different ways. Typically, computational performance, being governed by miniaturization of VLSI manufacturing process geometries, improves more rapidly than communication performance. For large scale computation communication performance tends to be governed by system integration constraints that are external to the chip, but with submicron manufacturing process nodes, even on-chip communication delays are impacting computational performance.
If we revisit the spatial graph of a parallel machine in our thought experiment, an improvement in the performance of the computation relative to the communication of information changes the trade-off between computation and communication in the parallel algorithm. In the vocabulary of spacetime, remote nodes move farther away.
Spacetime has a geometric interpretation of the relationship between space and time, called the spacetime light cone, as shown here:
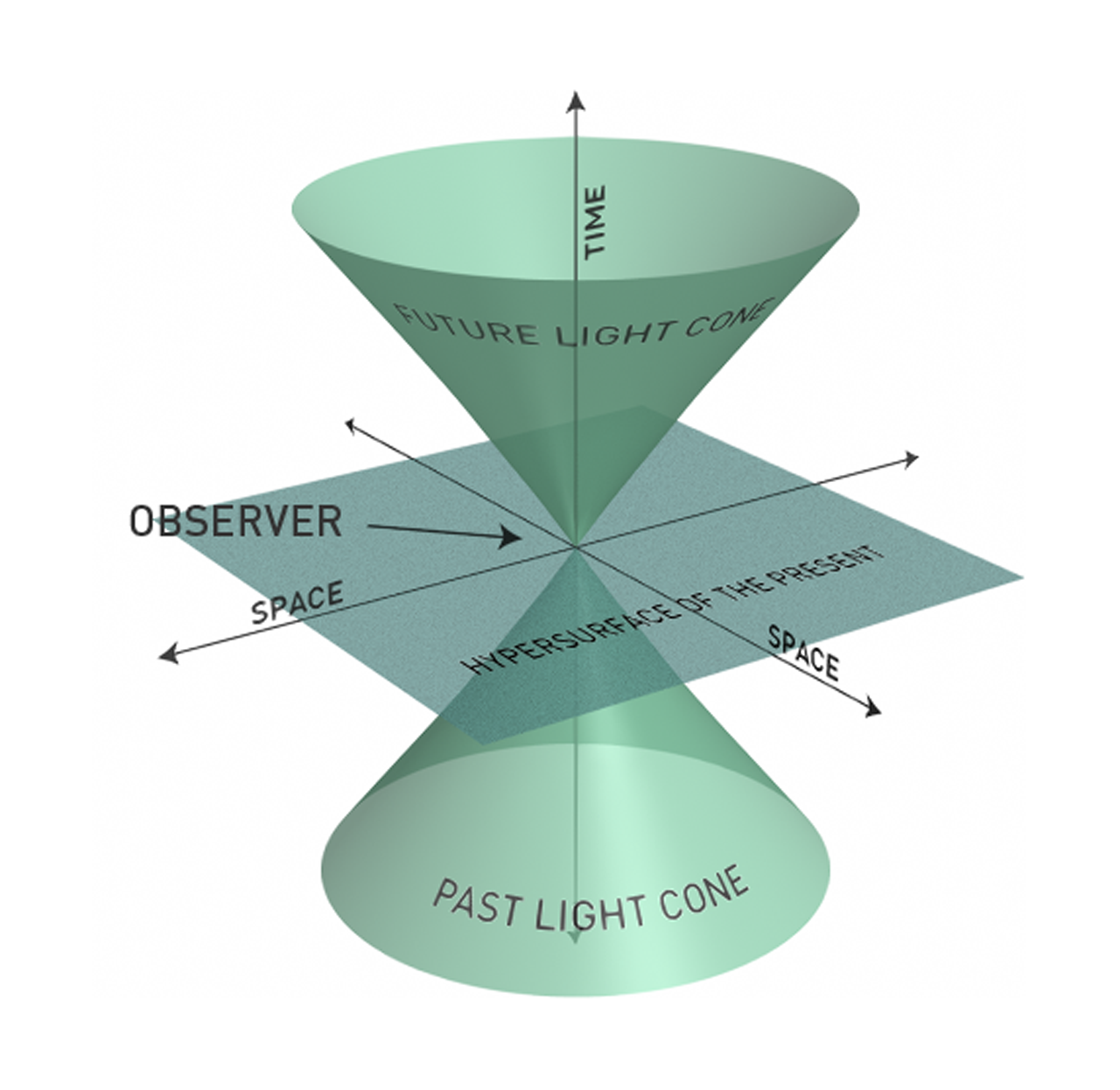
Spacetime Light Cone
The spacetime light cone is a visual mnemonic device to think about which events in spacetime can affect each other. Parallel computation requires the distribution of information and is thus constrained by the propagation of information. A computational event has to be able to ‘see’ its operands before it can commence. Otherwise stated, its operands need to lie in the future light cone.
These temporal constraints are further complicated by the fact that man-made structures today do not communicate through free space yet, and the physical communication structure adds additional constraints on the shape and extend of the future cone.
These man-made computational structures are dubbed computational spacetimes.